
중학생 딸이 학원에서 선행 학습으로 공통수학을 배우고 있다. 숙제가 많다면서, 열심히 공식을 외우면서 문제 풀이를 하고 있는데, 공식을 어떻게 나왔냐고 물어보니, 대꾸를 하지 않았다.(물론 공식 유도는 매우 골치아픈 일이긴 하다.)
점과 직선 사이의 거리와 관련된 내용이었는데,
유도 방법을 보니, 다음과 같았다.
1) 점과 직선의 최단 거리는 직각으로 만나야하고,
2) 이는 직선의 방정식(ax+by+c=0)과 최단거리로 표시되는 선분(AD)가 직각을 이뤄야 하므로,
3) 기울기 값으로 문제 풀이하는 방법을 확인할 수 있었다.
-. 직선의 방정식 기울기: -a/b
-. 선분AD의 기울기: b/a
-. 점A(x1, y1)을 지나고, 기울기가 b/a인 직선의 방정식
-. 상기 방정식과 ax+by+c=0의 만나는 점을 구한 후(연립일차방정식의 해)
-. 연립일차방정식의 해와 점A(x1, y1) 간의 거리 (두 점 사이의 거리)
생각보다 풀이 과정이 복잡해 보였다. 수학 문제는 답은 하나이되, 접근 방법은 다양할 수 있기에, 다른 방법으로 공식을 유도할 수 있지 않을까 생각을 해보았고, 피타고라스의 정리와 직각삼각형의 넓이를 이용해서, 공식을 유도해 보았다.
피타고라스의 정리


직각삼각형의 넓이

점과 직선 사이의 거리 공식 유도

점 B(x1,y1)과 직선 (ax+by+c=0)과 만나는 두 점을 A, C라고 하면, 두 점의 좌표는 다음과 같이 표시할 수 있다.

공식유도는 직각 삼각형의 넓이와 피타고라스의 정리를 활용하였다.
선분 AB의 길이와 선분 BC의 길이는 다음과 같고,

피타고라스의 정리를 활용하면, 선분 AC의 길이는 다음과 같다.

삼각형 ABC는 직각 삼각형이므로, 다음의 식이 성립한다. 여기서 선분 BD가 우리가 구하고자 하는 점과 직선 사이의 거리이다.


맺음말
학원에서 선행을 나가고 있으므로, 수업을 듣고 있겠지만, 중학생에게 고등수학은 이해의 영역을 넘어간다는 생각이 들었다. 왜냐하면, 진도에 뒤쳐지지 않기 위해서, 이해시키려고 노력해 보았지만, 쉽지 않았기 때문이다. 고민 끝에 내린 결론은, 일단 공식을 외워서 문제를 풀고, 학원 숙제를 마무리하는 것이었다. 이해의 유/무를 떠나서, 한번 풀어봤다는 생각이 다시 문제를 접할 때 좀 더 친숙하게 다가갈 수 있다면 그것만으로도 소기의 성과는 달성했다고 봐야하지 싶다.그리고, 이해는 다음번에 해도 충분히 늦지 않을 것이다.
(참고) 직교하는 두 직선을 활용한 점과 직선 사이의 거리 유도 방법






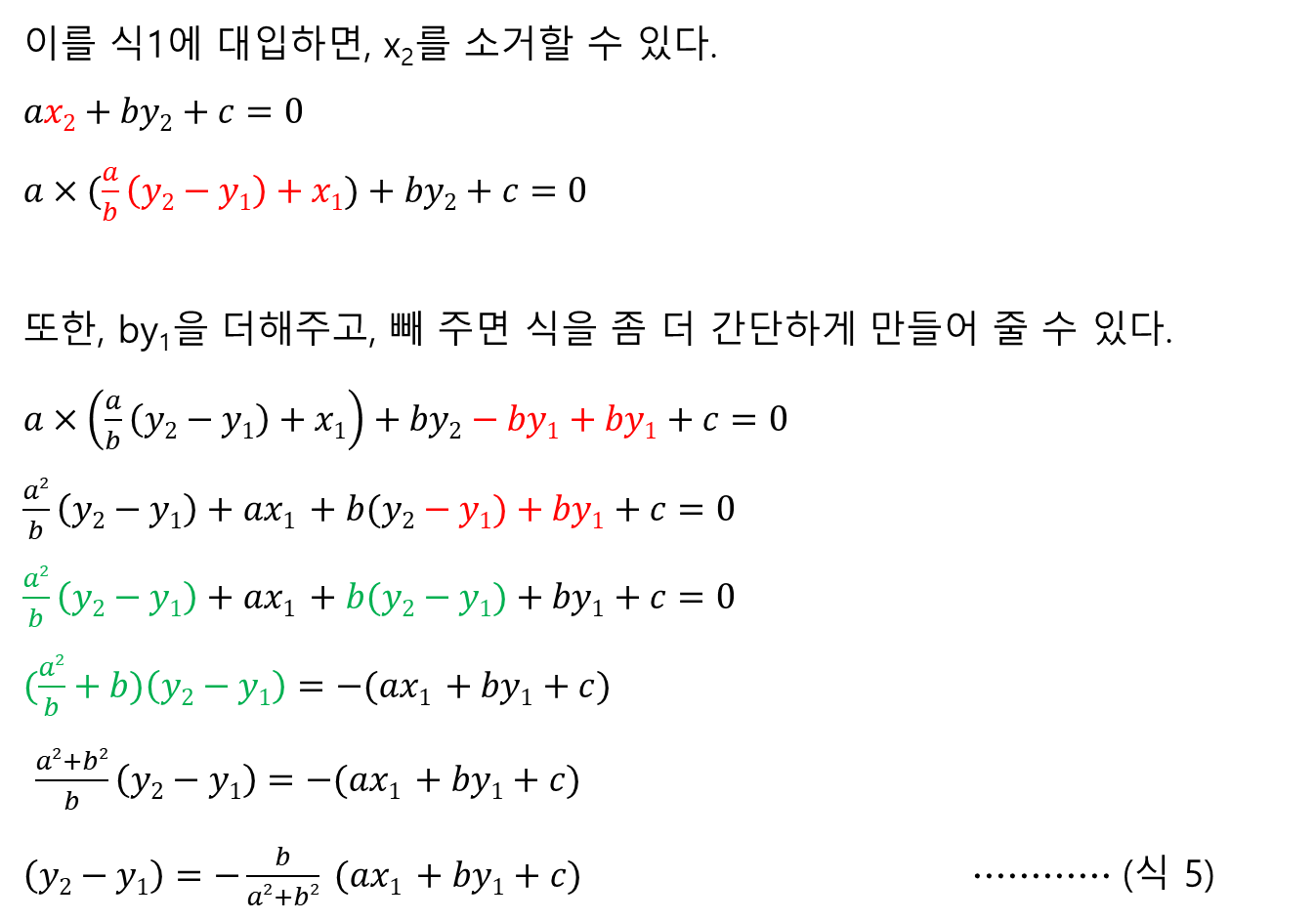
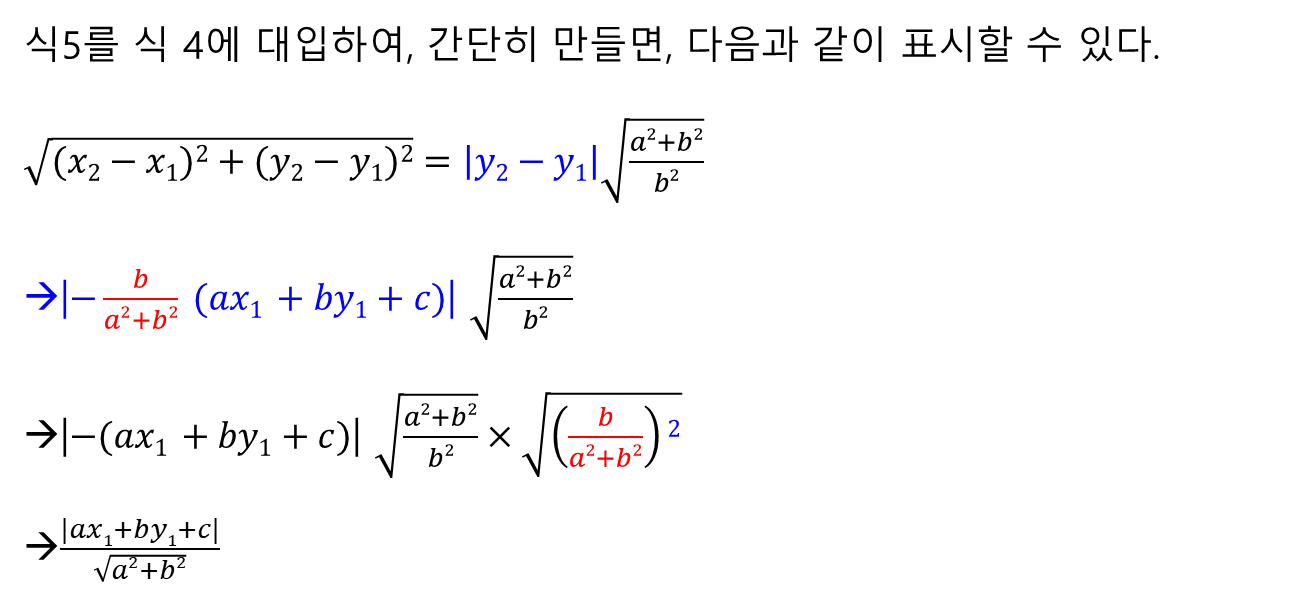

'자녀와 함께 (Study)' 카테고리의 다른 글
| (수학) 사선공식, 좌표평면, 삼각형 넓이 구하기 (6) | 2024.10.12 |
|---|---|
| 초등학교 6학년 영어 비교급 쉽게 이해하기 (0) | 2024.06.17 |
| 초등 고학년 독후감상문, 모든 길은 로마로_앗시리즈_240317 (0) | 2024.05.08 |
| 초등 고학년 독후감상문, 이왕이면 이집트_앗시리즈_240316 (0) | 2024.05.02 |
| 초등 고학년 독후감상문, 해리엇_240229 (1) | 2024.05.01 |




댓글